
DOI: https://doi.org/10.34069/AI/2025.86.02.19
Volume 14 - Issue 86: 250-263 / February-december, 2025
How to Cite:
Silgado-Tuñón, DA., Sureda, P., López-Flores, J.I., & Magallanes, E. (2025). Exploring university mathematics professors' perceptions and use of GenAI: a conceptual fields approach. Amazonia Investiga, 14(86), 250-263. https://doi.org/10.34069/AI/2025.86.02.19
Exploring university mathematics professors' perceptions and use of GenAI: a conceptual fields approach
Percepciones y el uso de IAGen en profesores universitarios de matemáticas desde Campos Conceptuales
Received: August 28, 2025 Accepted: October 20, 2025
Written by:
Denilsón Andrés Silgado-Tuñón
https://orcid.org/0009-0005-7098-5073
Maestro-Investigador en Matemática Educativa, Universidad Autónoma de Zacatecas, México. Email: denilson.silgado@uaz.edu.mx
Patricia Sureda
https://orcid.org/0009-0004-6223-4424
Doctora-Investigadora del Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Núcleo de Investigación en Educación Matemática (NIEM-CIC-UNCPBA), Instituto Superior de Ingeniería del Software (ISISTAN/CONICET-UNCPBA), Facultad de Ciencias Exactas, Universidad Nacional del Centro de la Provincia de Buenos Aires (UNICEN), Argentina. Email: psureda@niem.exa.unicen.edu.ar
José Iván López-Flores
https://orcid.org/0000-0003-2350-2647
Doctor-Investigador de la Unidad Académica de Matemáticas de la Universidad Autónoma de Zacatecas, Zacatecas, México. Email: jlopez@uaz.edu.mx
Emmanuel Magallanes
https://orcid.org/0000-0001-7571-1892
Doctor-Investigador de la Universidad Politécnica de Zacatecas, Ingeniería Industrial, Plan de Pardillo s/n., Parque Industrial, Fresnillo, México. Email: emagallanes@upz.edu.mx
Abstract
Generative Artificial Intelligence (GenAI) is rapidly transforming higher education, challenging traditional pedagogical norms, and prompting a re-evaluation of teaching and learning practices. This study analyzes the operational invariants guiding university mathematics professors' action schemes when interacting with GenAI, using the Theory of Conceptual Fields (TCF) as a theoretical framework. Semi-structured interviews were conducted with ten active university mathematics professors, focusing on the eight dimensions of Technological Pedagogical Content Knowledge (TPACK). Transcriptions were analyzed to infer enacted theorems (ETs), classified into eight thematic categories: general functionality, prompt construction, knowledge validation, academic applications, ethics and regulation, relationship with teaching and learning, teacher knowledge and use, and limitations and risks. Results revealed a predominantly pragmatic usage scheme, with GenAI perceived as a search engine, process optimizer, and code generator. However, contradictory ETs indicate that the conceptual field is still under construction. Teachers primarily use GenAI for text editing, content generation, and idea organization, but its direct classroom use remains limited. Epistemological ambivalence exists regarding Gen's authority, with concerns about errors. Ethical and regulatory issues are not yet central. Findings highlight the need for critical, reflective, and context-sensitive appropriation of GenAI in university mathematics education, supported by professional development and institutional policy.
Keywords: Artificial intelligence, Educational technology, Teacher education, Higher education, Cognition, Conceptual Fields.
Resumen
La Inteligencia Artificial Generativa (GenAI) está transformando rápidamente la educación superior, desafiando las normas pedagógicas tradicionales y motivando una reevaluación de las prácticas de enseñanza y aprendizaje. Este estudio analiza los invariantes operacionales que guían los esquemas de acción de los profesores universitarios de matemáticas al interactuar con la GenAI, utilizando como marco teórico la Teoría de los Campos Conceptuales (TCC). Se realizaron entrevistas semiestructuradas a diez profesores universitarios activos de matemáticas, centradas en las ocho dimensiones del Conocimiento Tecnológico Pedagógico del Contenido (TPACK). Las transcripciones fueron analizadas para inferir teoremas en acto (ETs), los cuales se clasificaron en ocho categorías temáticas: funcionalidad general, construcción de prompts, validación del conocimiento, aplicaciones académicas, ética y regulación, relación con la enseñanza y el aprendizaje, conocimiento y uso docente, y limitaciones y riesgos. Los resultados revelaron un esquema de uso predominantemente pragmático, con GenAI percibida como un motor de búsqueda, optimizador de procesos y generador de código. Sin embargo, los ETs contradictorios indican que el campo conceptual aún está en construcción. Los profesores emplean principalmente la GenAI para la edición de textos, generación de contenidos y organización de ideas, pero su uso directo en el aula sigue siendo limitado. Existe una ambivalencia epistemológica respecto a la confiabilidad de la GenAI, con preocupaciones sobre su propensión a cometer errores. Los marcos éticos y regulatorios aún no son centrales en el campo conceptual. Los hallazgos destacan la necesidad de una apropiación crítica, reflexiva y sensible al contexto de la GenAI en la educación universitaria en matemáticas, apoyada por el desarrollo profesional docente y la política institucional.
Palabras claves: Inteligencia artificial, Tecnología educativa, Formación docente, Educación superior, Cognición, Campos Conceptuales.
Introduction
The rapid evolution of GenAI models such as ChatGPT, Gemini, and Llama is transforming higher education by altering teacher–student–knowledge dynamics and opening new research lines (Silgado-Tuñón & López-Flores, 2025a). In this sense, generative systems not only facilitate problem solving, but also propose new forms of interaction with knowledge (Silgado-Tuñón & López-Flores, 2025b). Studies show that these chatbots can solve mathematical problems (Kang, 2024; Kwon et al., 2023; Sureda et al., 2024; Parra et al., 2024b; Corica et al., 2024) and adapt learning strategies (Lee et al., 2023), although their performance declines when using specific theoretical frameworks such as Brousseau’s Theory of Didactical Situations (Parra et al., 2024a). The ability of these LLMs to design tasks, generate explanations, and propose solutions raises challenges concerning the reliability and rigor of content. Thus, integrating GenAI requires not only adoption but also a broader pedagogical and ethical re-evaluation. It affects curriculum design, use as a didactic resource, assessment methods, and university policies (Larico-Hanco, 2024).
Recent studies reveal that professors express contradictory beliefs about GenAI: while most are familiar with these tools and 72% have experimented with them (Ruediger et al., 2024), few feel confident about their effective incorporation into teaching. Only a minority (14–18%) felt confident or understood its pedagogical applications, while many (38%) expressed little or no confidence. No individual use case has been established, suggesting that adoption is more exploratory than fully integrated.
Professors highlight GenAI’s usefulness for developing learning materials, creating assessments, personalizing content, supporting professional development, analyzing data, and assisting with administrative tasks (Alshamy et al., 2025; Larico-Hanco, 2024; Ruediger et al., 2024). Some studies suggest that GenAI can enhance academic performance, foster critical and creative thinking, and improve students’ understanding and production of texts (Larico-Hanco 2024). The emphasis on efficiency and content generation indicates that professors primarily perceive GenAI as a productivity tool for their existing work. While personalization is mentioned, the perceived benefits revolve around automation or assistance with labour-intensive tasks, which could free up time for more complex teaching activities but also brings the risk of reducing the human element in certain processes if not managed carefully.
Despite these benefits, teachers voice stronger concerns than students, particularly about academic misconduct such as plagiarism (Alshamy et al., 2025; Larico-Hanco, 2024). They fear excessive dependence that may erode critical thinking, creativity, and lead to superficial learning (Alshamy et al., 2025; Cabellos et al., 2024). Other challenges include biased or inaccurate information, unreliable citations, and the difficulty of distinguishing AI-generated from human work (Larico-Hanco, 2024). Some educators, especially in the humanities, worry that GenAI undermines trust in teaching practices, while others point to risks of widening inequality (Ruediger et al., 2024). Overall, integrity and critical thinking are perceived as core threats, explaining why 42% of instructors prohibit student use (Ruediger et al., 2024).
Objective of the study
The main objective of this study is to analyze the operational invariants that guide the action schemes of university mathematics teachers when interacting with GenAI, to inform adoption strategies and institutional policies.
This study analyzes the operational invariants guiding teachers’ action schemes with GenAI, aiming to inform adoption strategies and institutional policies.
Theoretical Framework
This study adopts Vergnaud’s Theory of Conceptual Fields (1990, 2013), which views knowledge as schemes constructed through action. We drew on two of Vergnaud’s four definitions of scheme.
Functional definition. A scheme is an invariant organization of behaviour in response to a family of situations.
Structural definition. The scheme is composed of (a) goals that guide the activity, (b) rules of action and control, (c) systems of representation, and (d) operational invariants.
Operational invariants include both operative concepts and operative theorems (OT). The former refers to relevant categories, evaluated not by their truth but by their usefulness in guiding action; the latter are propositions assumed as true during action. While both give meaning to the scheme, they differ from scientific concepts and theorems, which are explicit and subject to debate, whereas operational invariants usually remain implicit, forming the submerged part of the conceptual ‘iceberg.
Thus, the decisions a teacher makes in a didactic situation depend on the scheme activated, and on the operative concepts and theorems available to them. These invariants make it possible to select relevant information and, according to the goal, deduce the most appropriate rules of action (Vergnaud, 1990). In other words, they render the scheme operative.
When operative concepts and theorems are verbalized, they are transformed into objects for reflection, whose validity can be discussed, thus approaching scientific knowledge. Conversely, all formalized knowledge originates from these operational invariants, which are made explicit over time. However, formalized knowledge constitutes only a fraction of the knowledge that can be put into words. Vergnaud (2007a, 2007b) distinguishes two forms of knowledge: operative (acting effectively) and predicative (describing objects and relations).
This study examines professors’ explicit responses, thus focusing on the predicative dimension of knowledge, which offers only a partial view of the operative knowledge mobilized in teaching.
Methodology
We conducted semi-structured interviews with ten university professors from Mathematics, Physics, Engineering, and Science and Technology of Light and Matter (LUMAT) at a Mexican public university. All held doctorates and taught mathematics across different programs. The group included graduates in mathematics, physics, economics, agronomy, and computer systems.
Although their undergraduate backgrounds vary, all participants share a common professional denominator: they actively teach mathematics at the university level. This shared teaching practice legitimizes the focus of the study on their mathematical action schemes, since their daily instructional decisions and interactions are framed within the discipline of mathematics regardless of their original field of training.
Interviews lasted about 50 minutes and explored TPACK dimensions (Mishra & Koehler, 2006; Mishra et al., 2023), focusing on professors’ perceptions and uses of GenAI in mathematics teaching. Questions addressed familiarity with GenAI, prompt construction, applications in teaching and research, curriculum design, and perceptions of benefits, risks, and biases.
Interviews were transcribed with Whisper, organized with ChatGPT, and securely stored and processed in cloud services.
Table 1 illustrates how episodes were constructed and how enacted theorems (ET) were inferred. The excerpt corresponds to Interviewee P1, a professor with 12 years of experience and advanced training in mathematics. His statements on the use of GenAI in the classroom were coded into ETs, such as ‘GenAI works as a search engine’ or ‘GenAI is an image generator.’ Each episode (E) denotes a speaking turn, and the corresponding ET reflects the researcher’s analytical inference from the professor’s responses.
Table 1.
Example excerpt corresponding to Interviewee P1.

After coding all interviews, the ETs were classified into eight thematic categories: (1) general functionality, (2) prompt construction, (3) authority and validation, (4) academic and educational applications, (5) ethics and regulation, (6) teaching and learning relationships, (7) teacher knowledge and use, and (8) limitations and risks. For each ET, we recorded its number, description, frequency, validity, and category. The following section presents the tables organized by category.
Results and Discussion
In the first category, related to the general functionality of GenAI, the enacted theorems concerning what GenAI is and what it can do are grouped together; this category includes enacted theorems linked to its operational definition, technical capabilities, and general limitations.
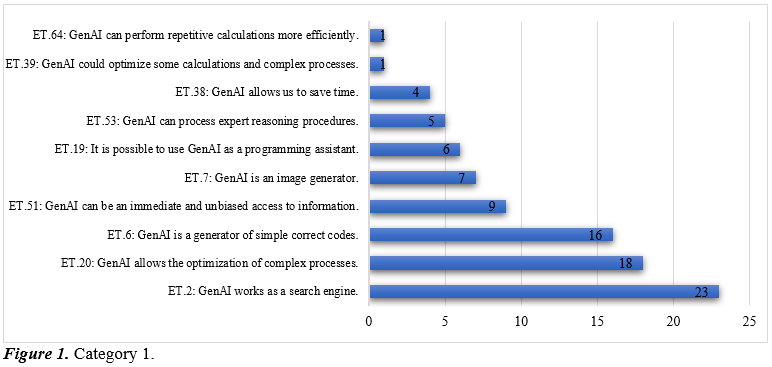
The results reveal that, within the conceptual field of university mathematics professors, a pragmatic usage scheme predominates. A core group of enacted theorems guides interaction with the tool: ET.2 (GenAI works as a search engine), ET.20 (GenAI allows the optimization of complex processes), and ET.6 (GenAI generates simple correct codes). These invariants frame GenAI as a rapid source of information, a resource for refining procedures, and a support for basic code production. From the perspective of the Theory of Conceptual Fields, this hierarchy reflects professional practices—information search, algorithmic modelling, and code prototyping—that have crystallized into stable schemes.
At the same time, the validity of these theorems is contested. ET.2 is problematic because AI responses are not equivalent to those of a search engine, and ET.6 requires caution since generated codes are not always correct. This tension highlights the need to qualify the authority of pragmatic uses.
Less frequent theorems point to incipient expansions. ET.51 describes GenAI as unbiased information access, ET.7 as an image generator, and ET.19 and ET.53 as a programming assistant and processor of reasoning. These open the possibility of collaborative or epistemic roles. By contrast, ET.38, ET.39, and ET.64, which link GenAI to numerical automation, remain marginal, reflecting the tool’s current limitations in mathematical reasoning (Sureda & Otero, 2025).
Overall, this category shows a conceptual field still under construction: pragmatic uses dominate, while explorations into more advanced or epistemic applications are emerging but not yet consolidated. For the second category, relating to the use and construction of Prompts, the enacted theorems concerning how to interact with GenAI are grouped; Figure 2 presents the frequency of the enacted theorems in this category.
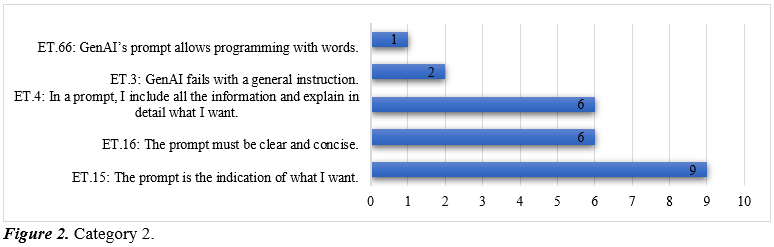
The data show that, within the conceptual field of prompt construction, teachers have stabilized a scheme centered on clarity of objectives and syntactic precision. The most frequently enacted theorem, ET.15 (The prompt is the indication of what I want), operates as an invariant guiding activity: the prompt is conceived as the tool that channels GenAI’s action. Two additional theorems highlight a central tension. ET.16 (The prompt must be clear and concise) reflects a search-engine logic, where brevity ensures results, while ET.4 (The prompt must include all information and detail) aligns with conversational interaction with GenAI and points to the need for greater specificity. From the perspective of the Theory of Conceptual Fields, these theorems define the tacit rules of the main scheme and reflect recurrent situations of interaction that ensure its viability.
Less frequent theorems expand this field. ET.3 (GenAI fails with a general instruction) acts as a metacondition of validity, underscoring the importance of specificity and triggering restructuring when responses lack relevance. ET.66 (Prompting is programming with words) suggests an exploratory view of prompt syntax as a form of high-level code, pointing toward more formalized practices of “linguistic programming.”
Overall, this category reveals a diversity of conceptions regarding prompt construction, ranging from minimal clarity to exhaustive detail. These distinctions carry direct implications for the communicative and pedagogical effectiveness of GenAI in educational contexts.
Category 3, called Authority and Validation of Knowledge, relates to the trust, validity, and verification of the responses provided by different GenAI tools. This category encompasses representations regarding the reliability of the generated information, the epistemological authority attributed to the tool, and the demands for critical judgment required for its educational application.
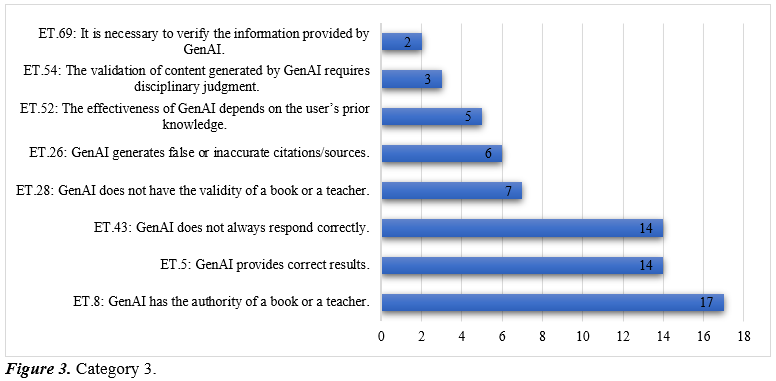
The results show a clear tension in the conceptual field of university mathematics professors regarding the epistemological status of GenAI. The most frequent enacted theorems are ET.8 (GenAI has the authority of a book or teacher), ET.5 (GenAI provides correct results), and ET.43 (GenAI does not always respond correctly). This contradiction reflects conceptual ambivalence: while the tool is perceived as a reliable source comparable to disciplinary knowledge, its propensity for errors is also recognized.
From the perspective of the Theory of Conceptual Fields, this can be read as the coexistence of contradictory yet un-stabilized schemes. The strong presence of ET.8 and ET.5 suggests a process of naturalizing GenAI’s authority, possibly encouraged by the fluency with which it presents answers. In contrast, ET.43 functions as a control mechanism, questioning that authority and fostering a more reflective stance. This unstable balance between trust and suspicion indicates a conceptual field still in reorganization.
Other theorems reinforce the need for validation. ET.28 (GenAI does not have the validity of a book or teacher) and ET.26 (GenAI generates false or inaccurate references) respond directly to technical limitations such as hallucinations and fabricated sources. Less frequent theorems—ET.52 (Effectiveness depends on the user’s prior knowledge), ET.54 (Validation requires disciplinary judgment), and ET.69 (Information must be verified)—emphasize the teacher’s role as epistemologically active agent, responsible for comparing, correcting, and contextualizing outputs.
Overall, this category reveals a conceptual field in dispute, where naive representations of GenAI’s authority coexist with critical stances demanding verification and expert judgment. Effective integration in university classrooms appears to depend on moving from automatic trust toward a reflective, epistemologically grounded use.
Category 4: Academic and Educational Applications pertains to the use of GenAI by professors in both their personal and professional activities. This category encompasses representations concerning text editing, the generation of teaching materials, idea organization, lesson planning, and assistance with evaluation tasks.
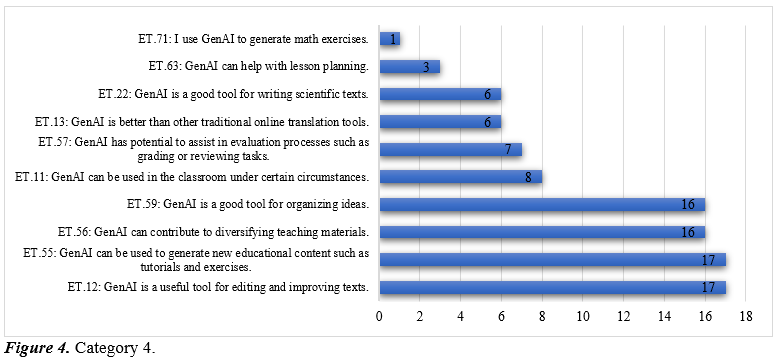
The results indicate that university mathematics professors attribute multiple academic support functions to GenAI. The most frequently enacted theorems are ET.12 (GenAI is useful for editing and improving texts) and ET.55 (GenAI can generate new educational content such as tutorials and exercises), closely followed by ET.56 (GenAI diversifies teaching materials) and ET.59 (GenAI helps organize ideas). Together, these theorems frame GenAI as a versatile assistant for text production and content structuring. From the perspective of the Theory of Conceptual Fields, they constitute a stabilized usage schema centered on productivity and efficiency. GenAI is not restricted to classroom application but extends to preparation and organizational tasks, functioning as an extension of teaching work.
Other theorems broaden this field. ET.11 suggests limited classroom use, while ET.57 (GenAI assists in evaluation, e.g., grading or reviewing) and ET.13 (GenAI improves on traditional translation tools) reflect its adoption for automated or technical tasks, reinforcing its utility in academic management.
More specialized theorems indicate exploratory moves toward discipline-specific use. ET.22 frames GenAI as a tool for scientific writing, ET.63 as support for lesson planning, and ET.71 as a generator of math exercises. These applications demand greater intellectual rigor and pedagogical contextualization, but their low frequency suggests that this transition remains incipient.
Overall, this category depicts a conceptual field dominated by technical and organizational uses, focused on improving academic products and optimizing routine tasks. Signs of a more didactic and discipline-specific appropriation are present yet marginal. Consolidating GenAI as an effective ally in mathematics teaching will likely depend on expanding these advanced uses and critically integrating them into planning and assessment.
Category 5, related to Ethics, Regulation, and Plagiarism—referring to responsibility, appropriate use of GenAI, and the standards that should govern its use— gathers representations related to human supervision, regulatory frameworks, authorship of work, and misuse of the tool.
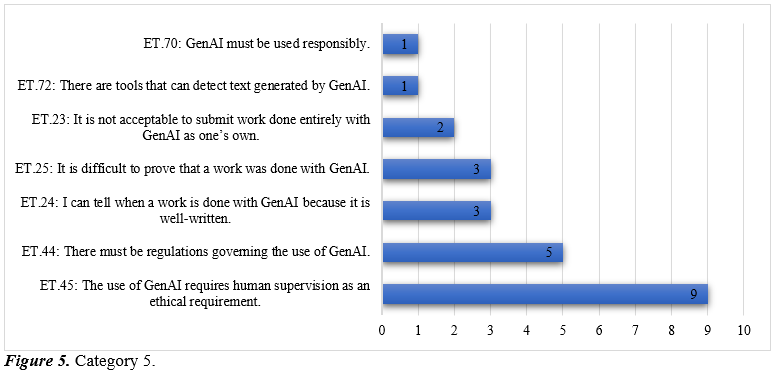
The results reveal an emerging, though still incipient, concern about the ethical use of GenAI in academia. The most frequent enacted theorems highlight that its use requires human supervision (ET.45) and must be governed by regulations (ET.44). Both indicate the perception that GenAI cannot be deployed outside an ethical and legal framework that ensures responsible use. From the perspective of the Theory of Conceptual Fields, these theorems represent regulatory invariants that remain under construction. Their low frequency compared to other categories shows that ethics is not yet central in professors’ conceptual field, though it is beginning to gain relevance as a necessary component of pedagogical practice.
Other theorems focus on plagiarism. ET.24 (I can tell when a paper was done with GenAI because it is written) and ET.25 (It is difficult to prove a paper was done with GenAI) reveal tension between intuitive detection and the practical difficulty of verification. These highlight unresolved questions about authorship, assessment, and originality.
Less frequent theorems reinforce academic integrity, such as ET.23 (It is not acceptable to submit a paper fully generated with GenAI), ET.72 (There are tools that can detect AI texts), and ET.70 (GenAI must be used responsibly). Although rare, they indicate the emergence of an implicit regulatory framework where acknowledgment, moderation, and external control are considered necessary for legitimate use.
In summary, this category reflects an ethical awareness that is still peripheral but growing. Professors recognize the importance of norms and principles, yet these have not been consolidated as structural elements of their professional practice. Consolidation of this ethical dimension will depend on institutional regulation and pedagogical strategies that foster responsible, transparent, and critical use of GenAI.
Category 6, called Relationship with Teaching and Learning, relates to the effect of using GenAI in educational settings linked to the teaching and learning process. This category includes enacted theorems that address its integration as a didactic tool, its impact on conceptual and procedural understanding, and the transformation of the traditional roles of teachers and students.
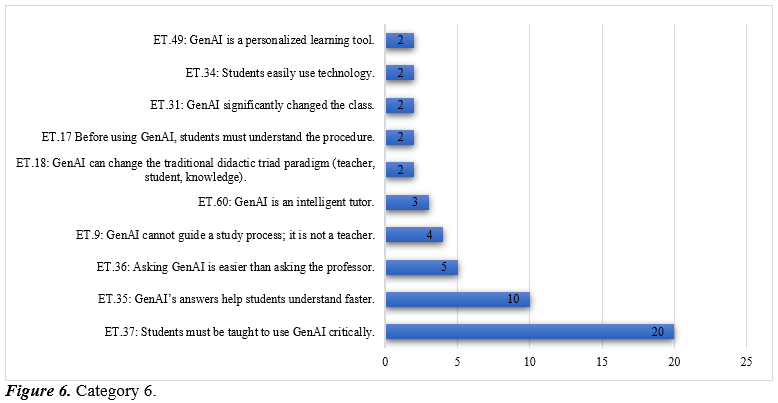
The results show a nuanced perception among university mathematics instructors regarding the incorporation of GenAI into teaching. The most frequently enacted theorem is ET.37 (Students must be taught to use GenAI critically), highlighting concern for developing critical literacy and avoiding unreflective dependence. This points to an emerging recognition that competencies for ethical and thoughtful use must be deliberately fostered.
Other theorems reveal positive yet ambivalent experiences. ET.35 (GenAI’s answers help students understand faster) and ET.36 (Asking GenAI is easier than asking the professor) suggest enhanced comprehension but also raise questions about the devaluation of direct pedagogical relationships. This duality indicates a transformation in classroom communication, where GenAI begins to function as an accessible cognitive mediator.
Tensions also appear between GenAI as support and its inability to replace human mediation. ET.9 asserts that it cannot guide a study process, while ET.60 frames it as an intelligent tutor. Together, these positions underline that while GenAI can assist in specific tasks, it is not perceived as a substitute for sustained educational guidance.
Less frequent theorems—ET.18 (GenAI may change the didactic triangle), ET.17 (Students should understand the procedure before using GenAI), and ET.31 (GenAI greatly changed the class)—reflect early explorations of epistemological and methodological transformation, as well as conditions for valid didactic use. ET.34 (Students use technology easily) and ET.49 (GenAI supports personalized learning) reinforce perceptions of accessibility and adaptation, though still at an early stage.
Taking together, this category depicts a transitional conceptual field, where enthusiasm for efficiency and accessibility coexists with the need to construct a critical pedagogical framework to guide integration. From the perspective of the TCF, usage schemes remain heterogeneous but teaching students how to use GenAI critically emerging as a necessary component of mathematics education.
Category 7 relates to GenAI Knowledge and Use by Instructors, which groups ET concerning teachers’ attitudes, experiences, and challenges. This category addresses aspects related to both the degree of technological adoption and the cognitive, emotional, or generational barriers mediating its integration into teaching practices.
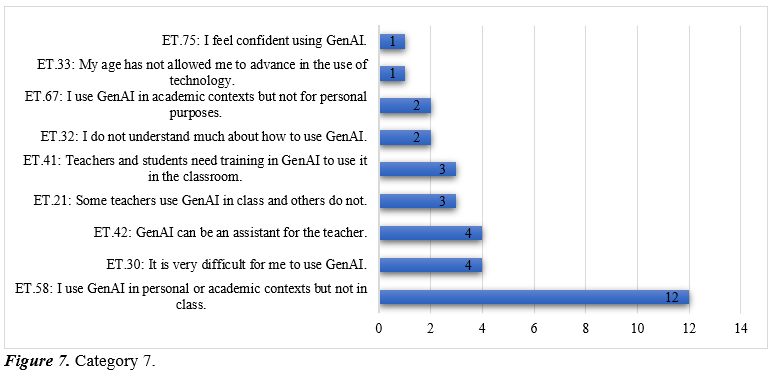
The results reveal an unequal and fragmented appropriation of GenAI among university mathematics faculty. The most frequent enacted theorem is ET.58 (I use GenAI personally or academically but not in class), which underscores the gap between private and pedagogical use. Although teachers recognize its potential, they face didactic, institutional, or epistemological barriers that limit integration into classroom practice.
Other theorems reflect ambivalence. ET.30 points to difficulties in using GenAI, while ET.42 highlights its value as an assistant for teaching work. This duality appears linked to varying levels of technological familiarity and the absence of training in pedagogical applications. ET.21 (Some teachers use GenAI in class and others do not) and ET.41 (Teachers and students need training to use it effectively) further emphasize the heterogeneity of adoption and the urgent need for professional development that promotes critical and context-sensitive appropriation.
Less frequent theorems reveal additional barriers. ET.32 (I do not understand much about GenAI), ET.67 (I use it academically but not personally), and ET.33 (My age prevents me from advancing with technology) point to cognitive, attitudinal, and generational limitations that create zones of resistance and insecurity. Addressing these requires institutional policies on digital inclusion. In contrast, ET.75 (I feel confident using GenAI) represents a minority of faculty who have advanced beyond the exploratory stage and achieved stable integration.
In summary, this category portrays an appropriation still in its early stages, where personal experiences disconnected from teaching, technological insecurity, and strong demands for training outweigh actual integration. From the perspective of the Theory of Conceptual Fields, usage schemes remain under construction, as individual and collective difficulties prevent the consolidation of shared operational invariants for systematic use.
Category 8, related to limitations and risks, groups together the enacted theorems related to errors, dependence, and problematic aspects of GenAI. This category gathers teacher representations that emphasize the cognitive, ethical, and functional boundaries of these technologies in education.
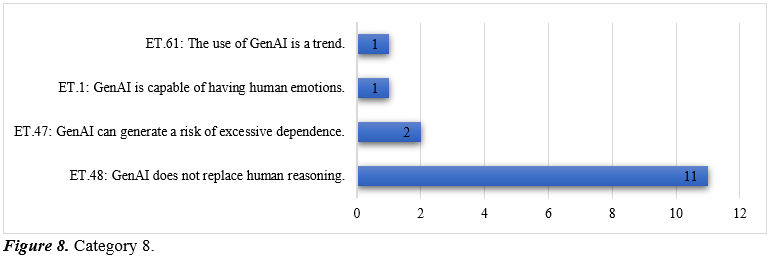
The results reveal that, although less frequently than in other categories, there is a clear conceptual core that identifies the epistemic boundaries of GenAI. The predominant enacted theorem is ET.48 (GenAI does not replace human reasoning), which synthesizes a critical stance among faculty: despite its technical potential, GenAI lacks the reflective, inferential, and metacognitive capacities inherent to human thought.
Its recurrence indicates that even frequent users remain aware of these limitations.
ET.47 (GenAI can generate excessive dependence) highlights concern about weakening autonomous thinking in teachers and students, raising risks of pedagogical de-professionalization and superficial learning.
Other theorems appear at the margins of the conceptual field. ET.1 (GenAI is capable of human emotions) reflects ontological confusion about its functioning, while ET.61 (The use of GenAI is a trend) reduces it to a passing fashion, potentially discouraging critical and sustained integration.
Together, these theorems indicate an incipient but firm framework that sets boundaries and anticipates risks. From the perspective of the Theory of Conceptual Fields, they operate as defensive schemes regulating responsible use. Although not yet a dominant core, their presence is essential to balance the utilitarian and enthusiastic views prevailing in other categories.
Taken together, the eight categories reveal that the conceptual field of university mathematics professors regarding GenAI is still in a phase of construction and reorganization. A pragmatic orientation dominates professors primarily using the tool as a search engine, process optimizer, and assistant for text and content production. These stabilized schemes reflect a strong focus on productivity and efficiency in academic work.
At the same time, other categories point to tensions and contradictions that limit homogeneous appropriation. On the one hand, there is a tendency to naturalize GenAI’s authority, treating it as a reliable source; on the other, various theorems stress its fallibility and the need for verification. This ambivalence illustrates the coexistence of un-stabilized schemes where trust and suspicion are balanced uneasily.
The categories also show incipient explorations beyond routine uses personalized learning, class planning, evaluation support, scientific writing, or programming assistance. Although still marginal, these theorems suggest a potential broadening of the field toward pedagogical innovation and discipline-specific applications. At the same time, limitations and risks—excessive dependence, ethical dilemmas, and ontological confusions—are acknowledged, shaping defensive schemes that temper enthusiasm with caution.
Overall, the results portray a fragmented and transitional field, where pragmatic appropriation coexists with emerging critical awareness. From the perspective of the Theory of Conceptual Fields, this configuration indicates that operational invariants have not yet been crystallized into a shared and stable framework. Instead, teachers navigate between efficiency-driven practices, ethical and epistemological concerns, and the challenge of integrating GenAI into mathematics education in a reflective and pedagogically grounded way.
General Discussion
Across the eight categories, a clear dialectic emerges between pragmatic and epistemological dimensions. On one side, professors’ predominant operational schemes reflect utilitarian uses of GenAI oriented toward productivity, optimization, and information retrieval. On the other, there is an emerging epistemic ambivalence that reveals reflective awareness about authority, validity, and ethical responsibility. This duality—between efficiency and critical caution—constitutes the core tension shaping teachers’ conceptual field.
From the perspective of Vergnaud’s Theory of Conceptual Fields, these results suggest that while pragmatic invariants (e.g., “GenAI provides correct results,” “GenAI works as a search engine”) have stabilized, epistemological and ethical invariants remain under construction. Teachers oscillate between trust and suspicion, adaptation and resistance, and their schemes evolve as they encounter new didactic and technological situations. Thus, the current conceptual field can be described as transitional: oriented toward practical benefit but increasingly open to epistemological and pedagogical reflection.
Limitations and Future Research
This study nevertheless presents limitations. The sample is limited to a specific group of mathematics professors, which restricts the generalizability of the findings. Furthermore, the research was conducted at a historical moment when GenAI models are rapidly evolving, meaning that the perceptions and practices documented here may change soon.
Finally, future research should explore longitudinally how these usage schemes evolve, compare GenAI appropriation across disciplines, and analyze its impact on concrete classroom practices and on students’ experiences. Such studies will advance a deeper understanding of the possibilities and limits of GenAI in higher education, as well as the conditions required for its ethical, critical, and pedagogically meaningful integration.
Conclusions
The findings show that the appropriation of GenAI by university mathematics professors is still in an incipient stage, marked by the tension between pragmatic uses oriented towards efficiency and the need to construct critical and ethically grounded frameworks. This situation not only reflects how teachers relate to emerging technologies but also highlights the broader challenges faced by higher education in integrating disruptive innovations into discipline-specific practices.
From a theoretical and methodological perspective, the application of the TCF made it possible to identify the operational invariants that structure teaching practices around GenAI. This approach proved useful for analyzing educational phenomena linked to technology, providing a framework that reveals both stabilized schemes and those still under reorganization. In this sense, TCF consolidates its value as an analytical tool capable of mapping conceptualization processes in less-explored areas, such as the relationship between teachers and artificial intelligence tools.
On a practical level, the results point to the urgency of developing teacher training programs that foster a critical, creative, and context-sensitive appropriation of GenAI. Such programs should balance the use of the tool for organizational and productivity tasks with the need to preserve cognitive autonomy, academic integrity, and pedagogical mediation. Likewise, institutional policies on digital inclusion are needed to address inequalities in access, knowledge, and teachers’ technological confidence.
These findings resonate with recent studies that also describe a fragmented and pragmatic appropriation of GenAI among faculty. Alshamy et al. (2025) and Larico-Hanco (2024) identified similar tendencies to rely on GenAI for organizational and technical tasks while showing hesitation to integrate it into the classroom.
Likewise, Ruediger et al. (2024) emphasized the persistence of ethical concerns and the limited pedagogical adoption of GenAI, consistent with the ambivalence documented here. The contribution of this study lies in extending these observations to the field of university mathematics education and in demonstrating, through the lens of the Theory of Conceptual Fields, how operational invariants emerge, stabilize, or remain in tension during the appropriation of disruptive technologies. This comparative dialogue underscores the need for cross-disciplinary research that examines both the common patterns and the domain-specific challenges of integrating GenAI into higher education.
Bibliographic references
Alshamy, A., Al-Harthi, A. S. A., & Abdullah, S. (2025). Perceptions of Generative AI Tools in Higher Education: Insights from Students and Academics at Sultan Qaboos University. Education Sciences, 15(4), 501. https://doi.org/10.3390/educsci15040501
Cabellos, B., de Aldama, C., & Pozo, J-I. (2024). University teachers’ beliefs about the use of generative artificial intelligence for teaching and learning. Frontiers in Psychology, 15, 1468900. https://doi.org/10.3389/fpsyg.2024.1468900
Corica, A., Parra, V., Sureda, P., Schiaffino, S., & Godoy, D. (2024). Fractal de Koch: análisis de respuestas de IA generativa y un profesor de matemática. Revista Iberoamericana de Tecnología en Educación y Educación en Tecnología (TE&ET), 89-99. https://doi.org/10.24215/18509959.37.e8
Kang, Y. J. (2024). A study on the didactical application of ChatGPT for mathematical word problem solving. Mathematical Education Communications, 38(1), 49-67. https://doi.org/10.7468/jksmee.2024.38.1.49
Kwon, O. N., Oh, S. J., Yoon, J. E., Lee, K. Y., Shin, B. C., & Jeong, W. (2023). Analyzing mathematical performances of ChatGPT: Focusing on the solution of national assessment of educational achievement and the college scholastic ability test. Mathematical Education, 37(2), 233-256. https://doi.org/10.7468/jksmee.2023.37.2.233
Larico-Hanco, R. (2024). Impacto de la Inteligencia Artificial Generativa Chatgpt en la Enseñanza Universitaria. Em SciELO Preprints. https://doi.org/10.1590/SciELOPreprints.9332
Lee, G. M., Lee, Y. J., & Kim, H. J. (2023). Analysis of adaptive learning in Korea's AI mathematics learning platforms. Journal of the Korean School Mathematics Society, 26(3), 245-268. https://doi.org/10.30807/ksms.2023.26.3.004
Mishra, P., & Koehler, M. J. (2006). Technological Pedagogical Content Knowledge: A Framework for Teacher Knowledge. Teachers College Record, 108(6), 1017-1054. https://doi.org/10.1111/j.1467-9620.2006.00684.x
Mishra, P., Warr, M., & Islam, I. (2023). TPACK in the age of ChatGPT and Generative AI. Journal of Digital Learning in Teacher Education, 39(4), 235-251. https://doi.org/10.1080/21532974.2023.2247480
Parra, V., Sureda, P., Corica, A., Schiaffino, S., & Godoy, D. (2024a). Can generative AI solve Geometry problems? Strengths and weaknesses of LLMs for geometric reasoning in Spanish. International Journal of Interactive Multimedia and Artificial Intelligence, 8(5), 65-74. https://doi.org/10.9781/ijimai.2024.02.009
Parra, V., Sureda, P., & Corica, A. (2024b). Teoría de Situaciones Didácticas e Inteligencia Artificial: diseño de propuestas para enseñar las nociones de muestra y población en educación secundaria. Uno: Revista de Didáctica de Las Matemáticas, (104), 43-50.
http://hdl.handle.net/11336/241263
Ruediger, D., Blankstein, M., & Love, S. J. (2024). Generative AI and Postsecondary Instructional Practices: Findings from a National Survey of Instructors. (Vol. 320892). Ithaka S+R. https://doi.org/10.18665/sr.320892
Silgado-Tuñón, D. A., & López-Flores, J. I. (2025a). Inteligencia Artificial Generativa en la Educación Superior: una Revisión Sistemática. Unión - Revista Iberoamericana de Educación Matemática, 21(73). Recuperado a partir de https://union.fespm.es/index.php/UNION/article/view/1709
Silgado-Tuñón, D. A., & López-Flores, J. I. (2025b). Inteligencia Artificial Generativa en el aula: ¿aliada o amenaza para la enseñanza de las matemáticas? Revista Electrónica Tecnologías Emergentes en la Educación, 2(1), 53-66. https://doi.org/10.71713/retee.v2i1.3512
Sureda, P., & Otero, M. (2025). Lo exponencial en la Escuela Secundaria de Adultos: análisis de invariantes operatorios. Educación matemática, 37(1), 101-126. https://doi.org/10.24844/EM3701.04
Sureda, P., Corica, A., Parra, V., Godoy, D., & Schiaffino, S. (2024). La evaluación en educación matemática: aportes de chatbots y futuros profesores de matemática. Edutec, Revista Electrónica De Tecnología Educativa, (89), 64-83. https://doi.org/10.21556/edutec.2024.89.3243
Vergnaud, G. (1990). La théorie des champs conceptuels. Recherches en Didactique des Mathématiques, 10(23), 133-170. https://acortar.link/MW7yqs
Vergnaud, G. (2007a). Forma operatoria y forma predicativa del conocimiento, en M. R. Otero, I. Elichirebehety, M. Fanaro, A. Corica y P. Sureda (eds.), Primer Encuentro Nacional sobre Enseñanza de la Matemática, Tandil, Buenos Aires, Argentina.
Vergnaud, G. (2007b). ¿En qué sentido la teoría de los campos conceptuales puede ayudarnos para facilitar aprendizaje significativo? Investigações em Ensino de Ciências, 12(2), 285-302. https://ienci.if.ufrgs.br/index.php/ienci/article/view/475
Vergnaud, G. (2013). Pourquoi la théorie des champs conceptuels? Journal for the Study of Education and Development, 36(2), 131-161. https://doi.org/10.1174/021037013806196283

https://amazoniainvestiga.info/ ISSN 2322- 6307
This article presents no conflicts of interest. This article is licensed under the Creative Commons Attribution 4.0 International License (CC BY 4.0). Reproduction, distribution, and public communication of the work, as well as the creation of derivative works, are permitted provided that the original source is cited.